§4  傅立叶变换

一、         傅立叶积分

    [傅立叶积分]  在任一有限区间[-l, l]上绝对可积的函数，可以求出它的傅立叶级数(本章§1，二)

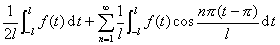                                            (1)

    设函数在无穷区间(- )上绝对可积，在(1)式中，令l，得出f ( x )的傅立叶积分

    [傅立叶积分的几种形式]

    设的傅立叶积分满足收敛的条件，那末

    1^o  =

    2^o  =  (外层积分理解为主值意义下的积分)

    3^o  是偶函数：

=

    4^o  是奇函数：

=

    [傅立叶积分的收敛判别法]  设函数在上绝对可积，记积分(1)的假想值为S₀.假设在点x₀连续，或者x₀是它的第一类间断点，并且在连续点x₀处S₀=，而在第一类间断点x₀处，

S₀=

    1^o  狄尼判别法 令，如果对于某,积分

收敛，那末的傅立叶积分在点x₀处收敛，并且等于S₀.

    2^o  狄利克莱-若当判别法  如果在以x₀为中点的某一区间[x₀-h,x₀+h]上有有界变差，那末它的傅立叶积分在点x₀处收敛，并且等于S₀.

    3^o  如果函数在上有有界变差，同时

那末的傅立叶积分在任一点x₀处收敛，并且等于S₀.