1. 行列式及其拉普拉斯展开定理
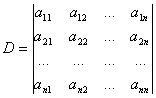
[n阶行列式] 设
是由排成n阶方阵形式的n2个数aij(i,j=1,2,...,n)确定的一个数，其值为n！项之和
式中k1,k2,...,kn是将序列1,2,...,n的元素次序交换k次所得到的一个序列，Σ号表示对k1,k2,...,kn取遍1,2,...,n的一切排列求和，那末数D称为n阶方阵相应的行列式.例如，四阶行列式是4！个形为
的项的和，而其中a13a21a34a42相应于k=3,即该项前端的符号应为
(－1)3.
若n阶方阵A=（aij）,则A相应的行列式D记作
D=|A|=detA=det(aij)
若矩阵A相应的行列式D=0，称A为奇异矩阵，否则称为非奇异矩阵.
[标号集] 序列1,2,...,n中任取k个元素i1,i2,...,ik满足
1≤i1<i2<...<ik≤n (1)
i1,i2,...,ik构成{1,2,...,n}的一个具有k个元素的子列，{1,2,...,n}的具有k个元素的满足(1)的子列的全体记作C(n,k),显然C(n,k)共有
个子列.因此C(n,k)是一个具有个元素的标号集（参见第二十一章，§1，二），C(n,k)的元素记作σ,τ,...,
σ∈C(n,k)表示
σ={i1,i2,...,ik}
是{1,2,...,n}的满足(1)的一个子列.若令τ={j1,j2,...,jk}∈C(n,k),则σ=τ表示i1=j1,i2=j2,...,ik=jk.
[子式 · 主子式 · 余子式 ·代数余子式]
从n阶行列式D中任取k行与k列（1≤k≤n－1）,由这k行与k列交点处的元素构成的k阶行列式称为行列式D的k阶子式，记作
,
σ,τ∈C(n,k)
如果所选取的k行k列分别是第i1,i2,...,ik行与第i1,i2,...,ik列，则所得到的k阶子式称为主子式.即当σ=τ∈C(n,k)时，
是主子式.
从行列式D中划去k行（σ）与k列（τ）后得到的n－k阶行列式称为子式的余子式，记作
.
如果σ={ i1,i2,...,ik}，τ={ j1,j2,...,jk}，则称
为子式的代数余子式.
特别，当k=1时，σ={i}，τ={j},子式就是一个元素aij,
aij的余子式记作
，aij的代数余子式记作Aij,即
且有 
（2）
或 
（3）
[拉普拉斯展开定理] 在n阶行列式D中任取k行（1≤k≤n-1）,那末包含于所选定的这些行中的所有k阶子式与它们各自的代数余子式的乘积之和等于行列式D，即对任意σ∈C(n,k)，1≤k≤n-1，
（4）
式中∑表示对标号集C(n,k)中的所有元素求和.
拉普拉斯定理中是对行进行的，对列有类似结果
（5）
此外还有
（6）
（7）
显然（2），（3）分别是（6），（7）的特例.
[拉普拉斯恒等式]
设A=(aij)m´
n,B=(bij) m´
n(m≥n),又设l=
,A的所有n阶子式为U1，U2，...，Ul，B的相应的n阶子式为V1,V2,...,Vl,则
det(AτB)=